이진검색(BinarySearch)
-
이진 검색(binary serch)은 요소가 오름차순 또는 내침차순으로
정렬되어 있는배열에서 검색하는 알고리즘이다. -
이진 검색은 선형 검색보다 좀 더 빠르게 검색할 수 있는 장점이 있다.
값을 찾는 경우
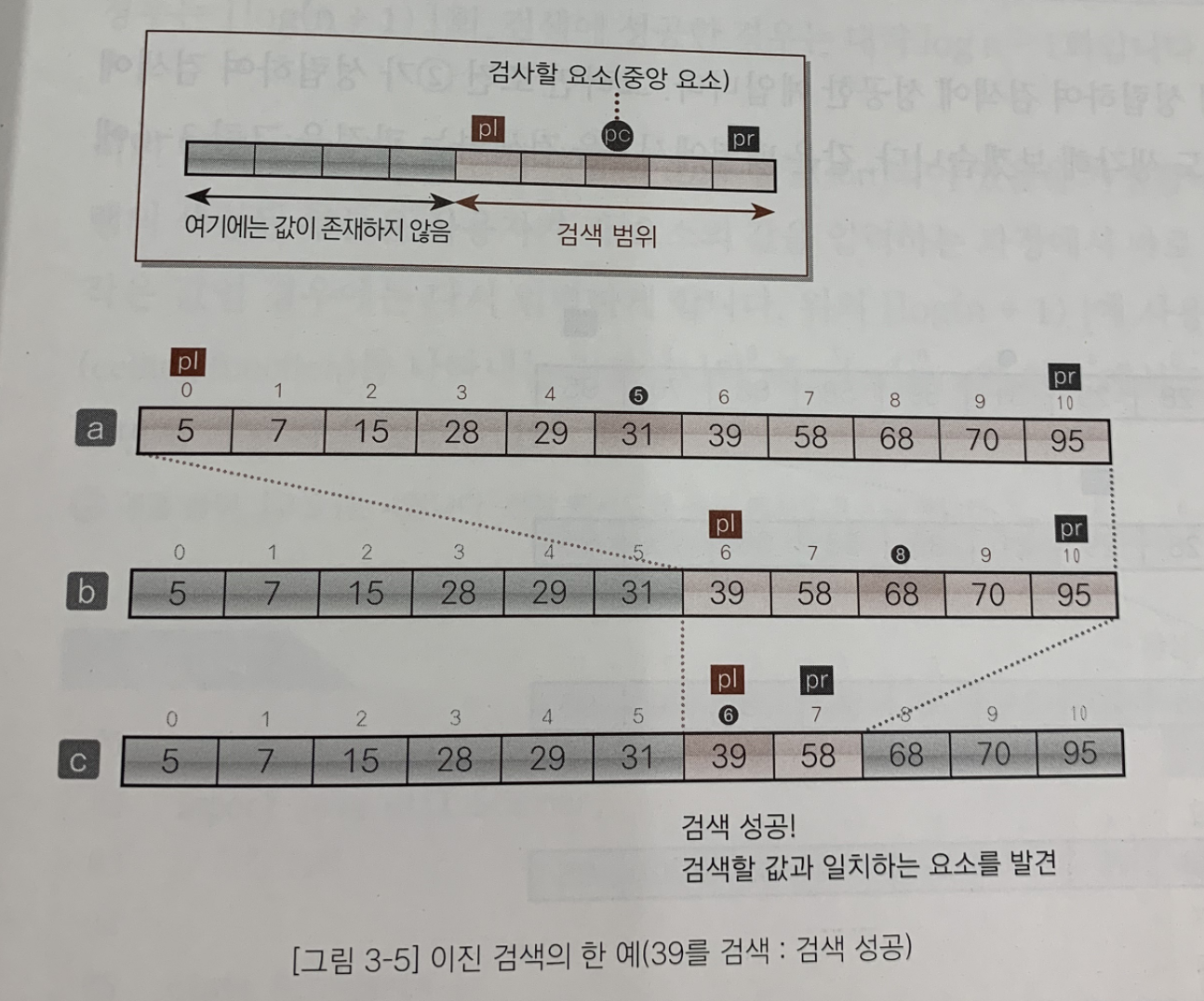
아래 그림에서 오름차순으로 정렬된 데이터에서 39를 검색하는 과정을 보자.
먼저 배열의 중앙에 위치한 요소인 a[5] 31부터 검색을 시작한다.

검색하려는 값인 39는 중앙 요소 a[5] 보다 큰 값이다.
그러므로 검색 대상을 뒤쪽의 5개 a[6] ~ a[10] 로 좁힐 수 있다.
그런다음 검색 범위의 중앙에 위치한 요소인 a[8] 68 이 원하는 값인지 확인한다.

검색하려는 값인 39보다 큰 값이다.
그러므로 검색 대상을 앞쪽의 2개 a[6] ~ a[7]로 좁힐 수 있다.
이제 검색해야 하는 대상은 2개인데 이때 두 요소의 중앙 요소는 39나 58 중 아무거나 택해도 상관없지만
여기서는 앞쪽의 값 39를 선택하여 원하는 값인지 확인한다. (두 인덱스 6과 7의 중앙값은 (6 + 7) / 2로 계산하여 6이 되기 때문이다.)

39는 원하는 키의 값과 일치하므로 검색 성공이다.
위와 같이 n개의 요소가 오름차순으로 늘어선 배열 a에서 키를 이진 검색으로 검색하는 과정을 표현해보자.
이때 검색 범위의
- 맨 앞 인덱스 : pl
- 맨 끝 인덱스 : pr
- 중앙 인덱스 : pc
라고 지정하며 검색을 시작할 때 pl은 0, pr은 n - 1, pc는 (n - 1) / 2 로 초기화 한다.
여기서 중요한 점은 이진 검색을 한 단계씩 진행할 때마다 검색 범위가 (거의)반으로 좁혀진다는 것이다.
또한 검사한 요소를 하나씩 제외시키는 선형 검색과는 다르게 이진 검색은 검색할 요소가 해당 단계에서 다음에 검색할 범위의 중간 지점으로 단숨에 이동한다.
이처럼 a[pc]와 key를 비교하여 같으면 검색은 성공이다.
원하는 값을 찾지 못한다면?
이진 검색을 하다가 원하는 값을 찾지 못하는 경우를 알아보자.
a[pc] < key 일 때
- a[pl] ~ a[pc]는 key보다 작은 것이 명확하므로 검색 대상에서 제외한다.
- 검색 범위는 중앙 요소 a[pc]보다 뒤쪽의 a[pc + 1] ~ a[pr]로 좁힙니다.
- 그런 다음 pl의 값을 pc + 1로 업데이트 한다.
a[pc] > key 일 때
- a[pc] ~ a[pr]은 key보다 큰 것이 분명하므로 검색 대상에서 제외한다
- 검색 범위는 중앙 요소 a[pc]보다 앞쪽 a[pl] ~ a[pc - 1]로 좁힌다.
- 그런 다음 pr의 값을 pc - 1로 업데이트 한다.
이진 검색 알고리즘의 종료 조건은 아래 조건중 하나만 성립하면 된다.
- a[pc]와 key가 일치하는 경우
- 검색 범위가 더 이상 없는 경우
아래 그림은 검색 실패의 예 이다.

a검색할 범위는 모든 배열 a[0] ~ a[10] 이고 중앙 요소 a[5]의 값은 31이다. 키 값인 6보다 크므로 검색 범위를 a[0] ~ a[4]로 좁힙니다.b새로 검색할 범위에서 중앙 요소의 값은 15 a[2] 입니다. 키 값인 6보다 크므로 검색할 범위를 a[0] ~ a[1]로 좁힌다.c새로 검색할 범위에서 중앙 요소의 값은 5 a[0] 입니다. 키 값인 6보다 작으므로 pl을 pc + 1로 즉 인덱스 1로 업데이트 한다. 그러면 pl과 pr은 1이된다.d축소된 범위의 중앙 요소의 값은 7 a[1]이다. 키 값인 6 보다 크므로 pr을 pc - 1 즉 인데스 0으로 업데이트 한다. 그러면 pl이 pr보다 커지면서 검색 범위를 더 이상 계산할 수 없게 된다. 종료 조건 2가 성립하므로 검색은 실패한다.
코드
import java.util.Scanner;
public class BinarySearch { // 이진 검색
// 요솟수가 n인 배열 a에서 key와 같은 요소를 이진 검색합니다.
static int binarySearch(int[] a, int n, int key){
int pl = 0; // 검색 범위의 첫 인덱스
int pr = n - 1; // 검색 범위의 끝 인덱스
do{
int pc = (pl + pr) / 2; // 중앙 요소의 인덱스
if(a[pc] == key)
return pc; // 검색 성공!
else if(a[pc] < key)
pl = pc + 1; // 검색 범위를 뒤쪽 절반으로 좁힘
else
pr = pc - 1; // 검색 범위를 앞쪽 절반으로 좁힘
}while (pl <= pr);
return -1; // 검색 실패!
}
public static void main(String[] args){
Scanner input = new Scanner(System.in);
System.out.print("요솟수 : ");
int num = input.nextInt();
int[] x = new int[num];
System.out.println("오름차순으로 입력하세요.");
System.out.print("x[0] : ");
x[0] = input.nextInt();
for (int i = 1; i < num; i++) {
do{
System.out.print("x[" + i + "] :");
x[i] = input.nextInt();
}while (x[i] < x[i - 1]);
}
System.out.print("검색할 값 : ");
int key = input.nextInt();
int idx = binarySearch(x, num, key);
if(idx == -1)
System.out.println("그 값의 요소가 없습니다.");
else
System.out.println(key + "은(는) x[" + idx + "]에 있습니다.");
}
}
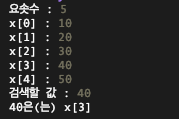
위 코드 실행 결과
선형검색 vs 이진검색
선형검색의 시간복잡도는 O(n)이고 이진검색의 시간복잡도는 O(log n) 이다.
시간복잡도만 보면 선형검색 보다 이진검색이 훨씬 좋아보인다.
차이점
- 선형 검색은 순차적 액세스를 수행하는 반면 이진 검색은 데이터를 임의로 액세스합니다.
- 선형 검색은 동등 비교를 수행하고 이진 검색은 순서 비교를 수행합니다.