큐(Queue)란?
- 큐는 스택과 마찬가지로 데이터를 일시적으로 쌓아 두기 위한 자료구조이다.
- 하지만 가장 먼저 넣은 데이터를 가정 먼저 꺼내는
선입선출(FIFO, First In First Out)인 점이 스택과 다르다. - 큐에 데이터를 넣는 작업을
인큐(enqueue)라 하고, 데이터를 꺼내는 작업을디큐(dequeue)라고 한다. - 인큐의 복잡도는 O(1)이고 디큐의 복잡도는 O(n)이다 디큐는 데이터를 꺼낼 때 다음 데이터를 앞으로 당기기 때문이다.
- 또한 데이터를 꺼내는 쪽을
프런트(front)라 하고, 데이터를 넣는 쪽을리어(rear)라고 한다.
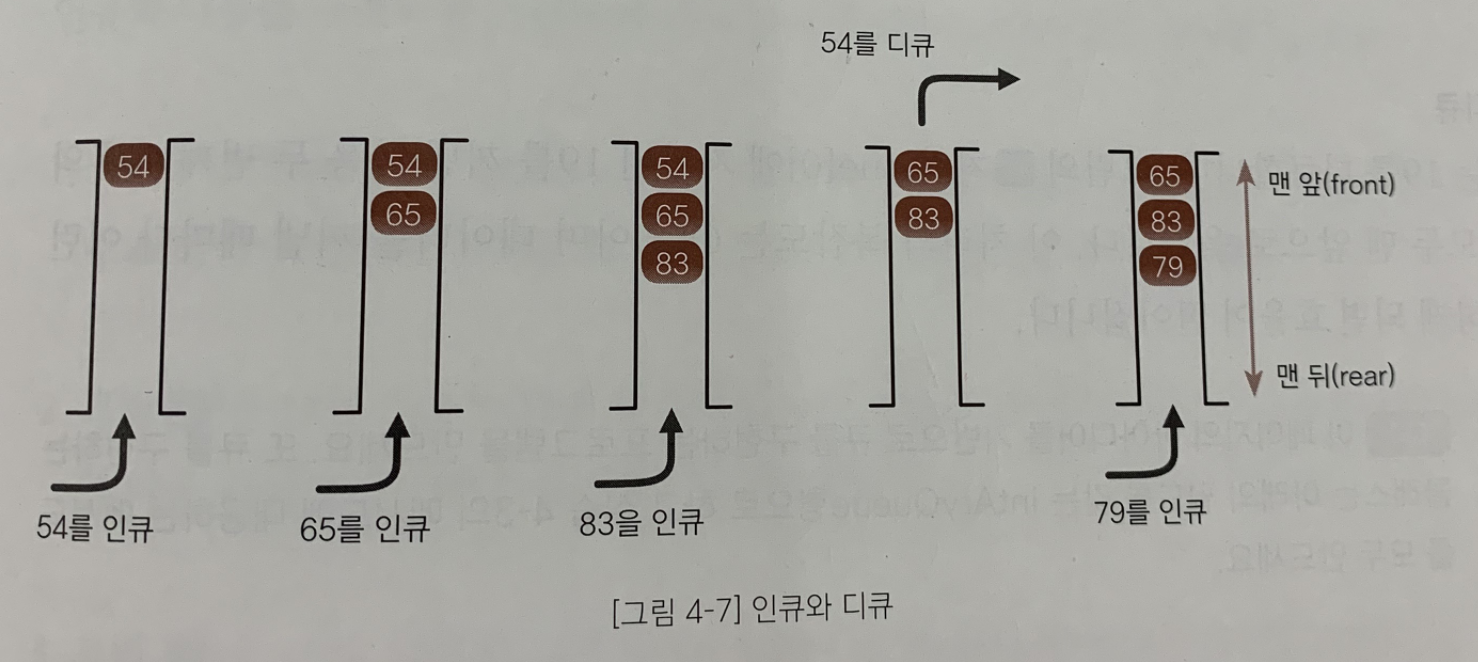
아래 그림은 큐의의 인큐와 디큐를 보여준다.
코드 (배열 활용)
import java.util.Scanner;
public class IntAryQueue { // int형 큐(링 버퍼(ring buffer)를 사용하지 않음)
private int max; // 큐 용량
private int num; // 현재 데이터 수
private int[] queue; // 큐 본체
// 생성자
public IntAryQueue(int capacity) {
max = capacity;
num = 0;
queue = new int[max];
}
// 실행 시 예외 : 큐가 비어 있음
public class EmptyIntQueueException extends RuntimeException {
public EmptyIntQueueException() {
throw new EmptyIntQueueException();
}
}
// 실행 시 예외 : 큐가 가득 참
public class OverflowQUeueException extends RuntimeException {
public OverflowQUeueException() {
throw new OverflowQUeueException();
}
}
// 인큐
public int InQueue(int data) {
if (num > max)
throw new OverflowQUeueException();
return queue[num++] = data;
}
// 디큐
public int DeQueue() {
if (num <= 0)
throw new EmptyIntQueueException();
int result = queue[0];
for (int i = 0; i < num - 1; i++)
queue[i] = queue[i + 1];
num--;
return result;
}
// 큐에서 데이터를 피크(머리 데이터를 살펴봄)
public int peek() throws EmptyIntQueueException {
if (num <= 0)
throw new EmptyIntQueueException(); // 큐가 비어 있음
return queue[num - 1];
}
// 큐에서 x를 검색하여 index(찾지 못하면 -1)를 반환
public int indexOf(int x) {
for (int i = 0; i < num; i++)
if (queue[i] == x) // 검색성공
return i;
return -1; // 검색실패
}
// 큐를 비움
public void clear() {
num = 0;
}
// 큐의 용량을 반환
public int capacity() {
return max;
}
// 큐에 쌓인 데이터 수를 반환
public int size() {
return num;
}
// 큐가 비어 있는가?
public boolean isEmpty() {
return num <= 0;
}
// 큐가 가득 찼는가?
public boolean isFull() {
return num >= max;
}
// 큐 안의 데이터를 머리→꼬리의 차례로 출력함
public void dump() {
if (num <= 0)
System.out.println("큐가 비었습니다.");
else {
for (int i = 0; i < num; i++)
System.out.print(queue[i] + " ");
System.out.println();
}
}
}
큐는 어디에 사용될까?
- 운영체제 작업 스케쥴링
- 대기행렬 처리
- 인쇄작업 대기목록
링 버퍼로 큐 만들기
- 이번에는 배열 요소를 앞쪽으로 옮기지 않는 링 버퍼 형태의 큐를 만들어 보자.
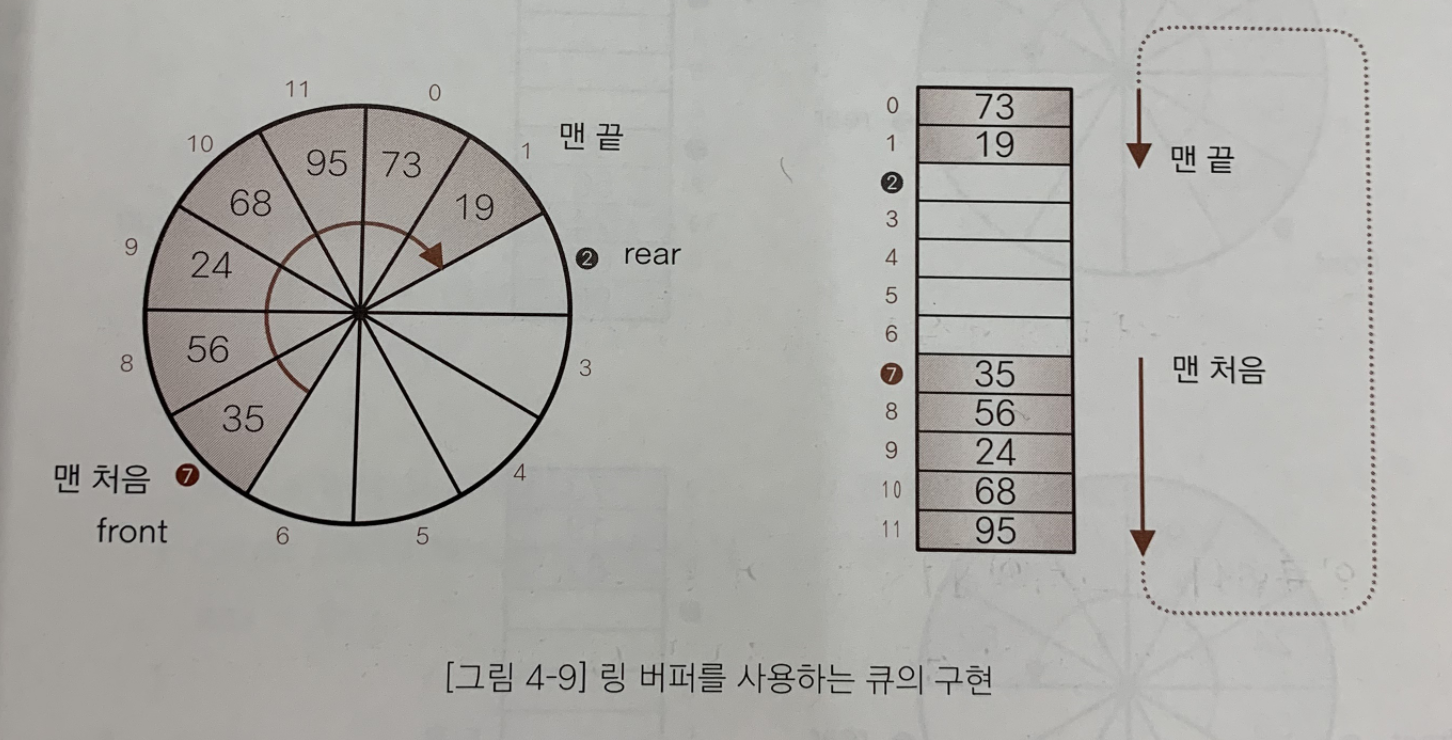
- 링 버퍼는 아래 그림과 같이 배열의 처음과 끝이 연결되어있는 자료구조 이다.
- 논리적으로 어떤 요소가 첫 번째 요소이고 어떤 요소가 마지막 요소인지 식별하기 위한 변수가
프런트(front)와리어(rear)이다.
프런트(front) : 맨 처음 요소의 인덱스 리어(rear) : 맨 끝 요소의 하나 뒤의 인덱스 (다음 요소를 인큐할 위치를 미리 지정)
코드 (링 버퍼로 큐 구현)
public class Queue<E> { // 링 버퍼 큐 구현
private int max; // 큐의 용량
private int num; // 현재 데이터 수
private int front; // 프런트 요소 커서
private int rear; // 리어 요소 커서
private E[] queue; // 큐의 본체
public static class OverflowQueueException extends RuntimeException{
public OverflowQueueException(){
throw new OverflowQueueException();
}
}
public static class EmptyQueueException extends RuntimeException{
public EmptyQueueException(){
throw new EmptyQueueException();
}
}
// 생성자
public Queue(int capacity){
num = front = rear = 0;
E[] queue = (E[]) new Object[capacity];
}
// 인큐
public E inque(E data) throws OverflowQueueException{
if(num >= max)
throw new OverflowQueueException();
E print = queue[rear++] = data;
num++;
if(rear == max) // rear와 max가 같아지면 rear 값이 배열의 없는 공간을 가르키게 된다.
rear = 0; // 그러므로 0으로 초기화
return print;
}
// 디큐
public E deque() throws EmptyQueueException{
if(num <= 0)
throw new EmptyQueueException();
E print = queue[front++];
num--;
if(front == max) // 인큐와 같은 인덱스 초과 문제를 막기 위함
front = 0;
return print;
}
// 큐에서 데이터를 피크(프런트 데이터를 들여다 봄)
public E peek() throws EmptyQueueException{
if(num <= 0)
throw new EmptyQueueException();
return queue[front];
}
// 큐에서 data를 검색하여 인덱스(찾지 못하면 -1)를 반환
public int indexOf(E data){
for (int i = 0; i < num; i++) {
int idx = (front + i) % max; // 스캔의 시작은 배열의 첫 요소가 아니라 큐의 첫 요소, 즉 프런트이기 때문이다.
if(queue[idx] == data)
return idx;
}
return -1;
}
// 검색
public int search(E data){
int number = 0;
for (int i = 0; i < num; i++) {
int idx = (front + i) % max;
number++;
if(queue[idx] == data)
return number;
}
return 0;
}
// 큐를 비움
public void clear() {
num = 0;
}
// 큐의 용량을 반환
public int capacity() {
return max;
}
// 큐에 쌓인 데이터 수를 반환
public int size() {
return num;
}
// 큐가 비어 있는가?
public boolean isEmpty() {
return num <= 0;
}
// 큐가 가득 찼는가?
public boolean isFull() {
return num >= max;
}
// 큐 안의 데이터를 머리→꼬리의 차례로 출력함
public void dump() {
if (num <= 0)
System.out.println("큐가 비었습니다.");
else {
for (int i = 0; i < num; i++)
System.out.print(queue[(front + i) % max] + " ");
System.out.println();
}
}
}
리뷰
개인적으로 코드에서 자세히 살펴봐야 할 부분을 다시 리뷰한다.
인큐
// 인큐
public E inque(E data) throws OverflowQueueException{
if(num >= max)
throw new OverflowQueueException();
E print = queue[rear++] = data;
num++;
if(rear == max) // rear와 max가 같아지면 rear 값이 배열의 없는 공간을 가르키게 된다.
rear = 0; // 그러므로 0으로 초기화
return print;
}
-
인큐에서 num이 max보다 크다면 예외를 던진다.
- 그렇지 않다면 큐에 데이터를 집어 넣고 rear값을 증가시킨다. (다음 인큐할 곳을 가르키기 위해)
if(rear == max) rear = 0;이 부분이 중요하다고 생각한다.- max값이 12이며 만약 인큐하기 전의 rear가 11이라고 가정해보자.
- 인큐 메서드를 수행한 다음에는 rear의 값이 12가 되면서 max값과 같아지는 문제가 발생한다.
- rear 값이 max와 같아지면 실제 배열에는 없는 공간인 queue[12]를 가리키게 됨
- 위와 같은 경우를 방지하기 위해 rear == max 이면 rear 를 0으로 초기화 해준다.
디큐
// 디큐
public E deque() throws EmptyQueueException{
if(num <= 0)
throw new EmptyQueueException();
E print = queue[front++];
num--;
if(front == max) // 인큐와 같은 인덱스 초과 문제를 막기 위함
front = 0;
return print;
}
- num이 0보다 작으면 예외를 던진다.
- front값을 증가시킨다.
- num값을 1 감소시킨다.
if(front == num) front = 0;- 여기서 인큐과 마찬가지로 인덱스 초과 문제가 발생한다.
검색 메서드 indexOf
// 큐에서 data를 검색하여 인덱스(찾지 못하면 -1)를 반환
public int indexOf(E data){
for (int i = 0; i < num; i++) {
int idx = (front + i) % max; // 스캔의 시작은 배열의 첫 요소가 아니라 큐의 첫 요소, 즉 프런트이기 때문이다.
if(queue[idx] == data)
return idx;
}
return -1;
}
아래의 그림으로 간단히 설명한다.

버퍼 링은 어디에 사용될까?
- 오래된 데이터를 버리는 용도
- 가장 최근에 들어온 데이터 n개만 저장하고 오래된 데이터는 버리는 용도로 사용한다.